PROPÓSITOS:
Que los alumnos obtengan la medida de la circunferencia y el diámetro de varios
círculos y adviertan que el cociente (El resultado de la división) del primero
sobre el segundo es una constante llamada pi (π)
Que reconozcan el producto obtenido entre π y la longitud del diámetro como un procedimiento más
para calcular la longitud de la circunferencia.
ACTIVIDAD N° 1
Lleva a cabo la siguiente actividad y después
contesta lo que se pide.
Toca el siguiente enlace para descargar la página del libro que ocuparemos.
Utiliza hilo o cuerda para medir la circunferencia y el diámetro de algunos
objetos circulares que tienes en tu casa (Plato, disco compacto, aro, una tapa,
etc.) y registren sus resultados en la tabla.
Después dividan la medida de la circunferencia (lo que mediste con el hilo
o cuerda) entre la medida del diámetro obtengan sus cocientes y completen la tabla;
pueden usar calculadora.
Escriban sólo dos cifras decimales para expresar el cociente.
Escriban sólo dos cifras decimales para expresar el cociente.
Ahora contesta las siguientes preguntas:
¿Cómo son los resultados de los cocientes?
¿A qué crees que se deba esto?
¿Cómo calculan la medida de la circunferencia si conocen la medida del
diámetro?
ACTIVIDAD N° 2
Ahora utilizarás la relación entre la circunferencia y el diámetro para resolver
los problemas de la lección 67.
Toca el siguiente enlace para descargar la página del libro que ocuparemos.
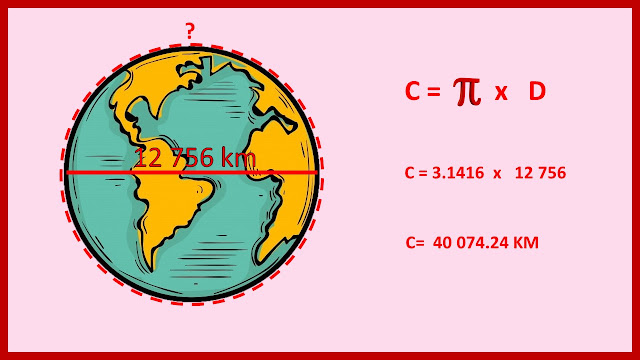
El primer problema se trata de calcular el valor de la circunferencia
utilizando el producto de π por la medida del diámetro. Se sugiere usar dos cifras decimales (3.1416) para el valor de π.
En el segundo, a diferencia del primero, se pide calcular el valor del
diámetro dado el valor de la circunferencia.
En el tercer problema, se calcula la longitud de la circunferencia y hay
que averiguar cuántas veces cabe ésta en 450 metros.














No hay comentarios:
Publicar un comentario